Overview
I developed a program in MIPS assembly language that performs multiplication operations on 3×3 matrices. This project required implementing fundamental matrix multiplication algorithms at the assembly level, dealing directly with memory management, register allocation, and low-level program flow control. The calculator efficiently handles the nine multiplication and addition operations required for each element in the resulting matrix.
Implementation
The program takes two 3×3 matrices as input and computes their product using nested loops. Each element in the result matrix is calculated by taking the dot product of the corresponding row from the first matrix and column from the second matrix. The implementation demonstrates efficient memory access patterns and register usage to optimize performance.
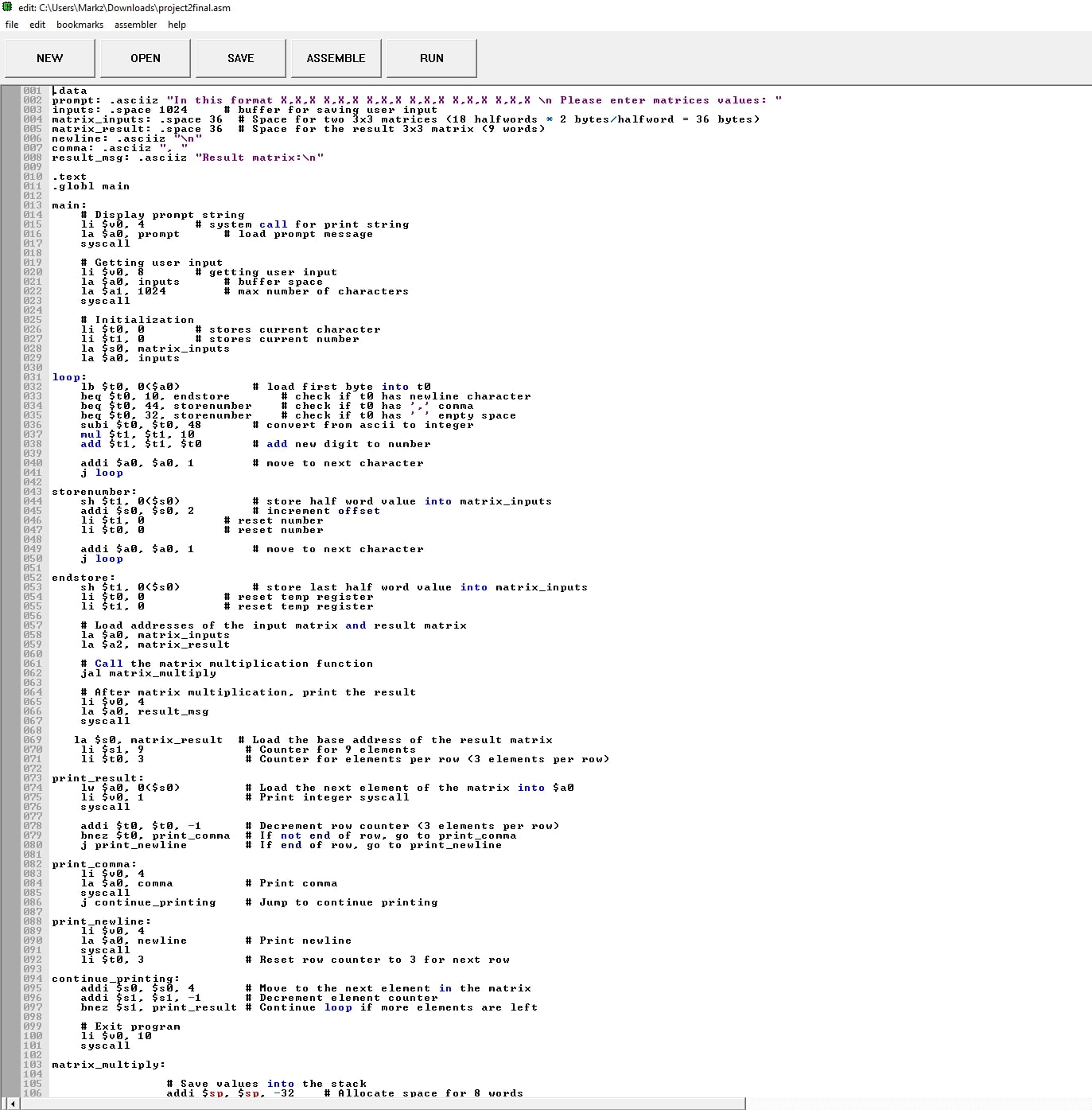
.data
prompt: .asciiz "In this format X,X,X X,X,X X,X,X X,X,X X,X,X X,X,X \n Please enter matrices values: "
inputs: .space 1024 # buffer for saving user input
matrix_inputs: .space 36 # Space for two 3x3 matrices (18 halfwords * 2 bytes/halfword = 36 bytes)
matrix_result: .space 36 # Space for the result 3x3 matrix (9 words)
newline: .asciiz "\n"
comma: .asciiz ", "
result_msg: .asciiz "Result matrix:\n"
.text
.globl main
main:
# Display prompt string
li $v0, 4 # system call for print string
la $a0, prompt # load prompt message
syscall
# Getting user input
li $v0, 8 # getting user input
la $a0, inputs # buffer space
la $a1, 1024 # max number of characters
syscall
# Initialization
li $t0, 0 # stores current character
li $t1, 0 # stores current number
la $s0, matrix_inputs
la $a0, inputs
loop:
lb $t0, 0($a0) # load first byte into t0
beq $t0, 10, endstore # check if t0 has newline character
beq $t0, 44, storenumber # check if t0 has ',' comma
beq $t0, 32, storenumber # check if t0 has ' ' empty space
subi $t0, $t0, 48 # convert from ascii to integer
mul $t1, $t1, 10
add $t1, $t1, $t0 # add new digit to number
addi $a0, $a0, 1 # move to next character
j loop
storenumber:
sh $t1, 0($s0) # store half word value into matrix_inputs
addi $s0, $s0, 2 # increment offset
li $t1, 0 # reset number
li $t0, 0 # reset number
addi $a0, $a0, 1 # move to next character
j loop
endstore:
sh $t1, 0($s0) # store last half word value into matrix_inputs
li $t0, 0 # reset temp register
li $t1, 0 # reset temp register
# Load addresses of the input matrix and result matrix
la $a0, matrix_inputs
la $a2, matrix_result
# Call the matrix multiplication function
jal matrix_multiply
# After matrix multiplication, print the result
li $v0, 4
la $a0, result_msg
syscall
la $s0, matrix_result # Load the base address of the result matrix
li $s1, 9 # Counter for 9 elements
li $t0, 3 # Counter for elements per row (3 elements per row)
print_result:
lw $a0, 0($s0) # Load the next element of the matrix into $a0
li $v0, 1 # Print integer syscall
syscall
addi $t0, $t0, -1 # Decrement row counter (3 elements per row)
bnez $t0, print_comma # If not end of row, go to print_comma
j print_newline # If end of row, go to print_newline
print_comma:
li $v0, 4
la $a0, comma # Print comma
syscall
j continue_printing # Jump to continue printing
print_newline:
li $v0, 4
la $a0, newline # Print newline
syscall
li $t0, 3 # Reset row counter to 3 for next row
continue_printing:
addi $s0, $s0, 4 # Move to the next element in the matrix
addi $s1, $s1, -1 # Decrement element counter
bnez $s1, print_result # Continue loop if more elements are left
# Exit program
li $v0, 10
syscall
matrix_multiply:
# Save values into the stack
addi $sp, $sp, -32 # Allocate space for 8 words
sw $s0, 28($sp)
sw $s1, 24($sp)
sw $s2, 20($sp)
sw $s3, 16($sp)
sw $s4, 12($sp)
sw $s5, 8($sp)
sw $s6, 4($sp)
sw $s7, 0($sp)
li $t7, 3 # just used for comparison
li $t0, 0 # loop counter
outer_loop: # this loop figures out which row of the first matrix and which column of the second will be in use
# t2 represents an intermediate for the position of the first value
li $t2, 0
# t5 represents an intermediate second value
li $t5, 0
li $t1, 0 # loop counter
inner_loop: # this loop figures out which element of the row/column is being multiplied
# operations on position of second value
move $t6, $t5
add $t6, $t6, $t0
add $t6, $t6, $t0
add $t6, $t6, $t0
# operations on position of first value
move $t4, $t2
add $t4, $t4, $t1 # this is to add the column position of the first value
li $t3, 0 # loop counter
li $s7, 0
iterate_both_positions: # reserved for the purposes of this loop: t0, t1, t2, t3, t4, t5, t6, t7
# final calculation for position in first matrix
li $s1, 0
move $s1, $t6
add $s1, $s1, $t3
sll $s1, $s1, 1 #half word align result
# final calculation for position in second matrix
li $s2, 0
move $s2, $t4
add $s2, $s2, $t3
add $s2, $s2, $t3
add $s2, $s2, $t3
addi $s2, $s2, 9
sll $s2, $s2, 1
#actual multiplication
li $s4, 0
li $s5, 0
add $s6, $s1, $a0 #Calculate effective address
lh $s4, 0($s6) # Load halfword from calculated address
add $s6, $s2, $a0 # Calculate effective address
lh $s5, 0($s6) # Load halfword from calculated address
mul $s3, $s4, $s5
add $s7, $s7, $s3
#final products go to 3 * outer_loop + inner_loop shifted left 2
li $s0, 0
add $s0, $t1, $t0
add $s0, $s0, $t0
add $s0, $s0, $t0
sll $s0, $s0, 2
# store s6 in stack because not enough registers
addi $sp, $sp, -4 # Adjust stack pointer
sw $s6, 0($sp) # Store $s6 on stack
add $s6, $s0, $a2 # Calculate effective address
sw $s7, 0($s6) # Store word at calculated address
lw $s6, 0($sp) # Load $s6 from stack
addi $sp, $sp, 4 # Restore stack pointer
addi $t3, $t3, 1
bne $t3, $t7, iterate_both_positions # end this loop if runs = 3
# increment runs
addi $t1, $t1, 1
bne $t1, $t7, inner_loop # end this loop if runs = 3
# increment runs
addi $t0, $t0, 1
bne $t0, $t7, outer_loop # end this loop if runs = 3
lw $s7, 0($sp)
lw $s6, 4($sp)
lw $s5, 8($sp)
lw $s4, 12($sp)
lw $s3, 16($sp)
lw $s2, 20($sp)
lw $s1, 24($sp)
lw $s0, 28($sp)
addi $sp, $sp, 32 # Deallocate space for 8 registers
jr $ra
Program Output
When executed, the program displays both input matrices and the resulting multiplication matrix:
Technical Challenges
Memory Management
Working with multi-dimensional arrays in MIPS assembly required careful address calculation to access the correct elements.
Solution: I implemented index calculations using multiplication and addition operations to convert 2D coordinates into linear memory offsets.
Register Allocation
MIPS has a limited number of registers, making it challenging to keep track of loop variables, addresses, and intermediate results.
Solution: I used a combination of temporary ($t) registers for short-lived values and saved ($s) registers for loop counters, properly saving and restoring context during function calls.
Nested Loop Implementation
Matrix multiplication requires three nested loops, which can be complex to implement in assembly language.
Solution: I structured the code with clear labels and branch instructions to maintain the loop hierarchy, making the control flow more readable and maintainable.
What I Learned
This project deepened my understanding of computer architecture principles, memory addressing, and low-level programming concepts. I gained valuable experience with:
- MIPS assembly language syntax and conventions
- Register allocation strategies
- Memory addressing techniques
- Implementation of mathematical algorithms at the assembly level
- Low-level optimization techniques